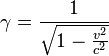Partial Derivatives

Ketika kita mempelajari kalkulus, kita tidak akan terlepas dari topik bernama "partial derivatives", karena topik ini adalah salah satu bagian dasar dari pembelajaran kalkulus.

Berbicara tentang turunan (derivative), katakanlah ada suatu fungsi f, yang apabila variabel-variabelnya bergerak, fungsi f juga ikut bergerak. Pertanyaannya sejauh mana dan seberapa cepat fungsi f bergerak seiring dengan pergerakan variabel-variabelnya? Itu akan terjawab lewat konsep turunan (derivative)

Mari bandingkan dua jenis fungsi yaitu fungsi dengan bentuk kurva (curve) dan fungsi dengan bentuk permukaan (surface)

 

Fungsi kurva y = f(x) vs fungsi permukaan z = f(x,y)

 

Dalam pembahasan ini, kita akan lihat hanya pada poin 1 yaitu partial derivatives

Mari lihat contoh cara derivasi partial

    Fungsi diatas jika diderivasikan secara parsial terhadap parameter x menjadi :

 

    dan jika diderivasikan secara parsial terhadap parameter y menjadi :

 

    Fungsi diatas jika diderivasikan secara parsial terhadap parameter x menjadi :

    dan jika diderivasikan secara parsial terhadap parameter y menjadi :

    Fungsi diatas jika diderivasikan secara parsial terhadap parameter T menjadi :

 

    dan jika diderivasikan secara parsial terhadap parameter V menjadi :

 

 

Sampai disini dulu saja pembahasan partial derivatives ya

Teori relativitas khusus

Teori ini menjelaskan bahwa benda yang bergerak dengan kecepatan mendekati kecepatan cahaya(c) akan mengalami perubahan relatif terhadap pengamat diam. Perubahan-perubahan tersebut meliputi panjang, massa, energi kinetik benda yang bergerak serta waktu yang dialami oleh benda yang bergerak relatif terhadap pengamat diam. Perubahan tersebut disebut juga sebagai dilatasi.

- Dilatasi panjang
Benda yang bergerak dengan kecepatan mendekati c akan mengalami perpendekan jika dilihat oleh pengamat diam.

L = panjang benda yang bergerak menurut pengamat diam
Lo = panjang benda sesungguhnya
Ada besaran yang gunanya untuk menghitung dilatasi waktu, panjang, dan massa. Karena v < c, maka nilai > 1.

- Dilatasi massa
Benda yang bergerak dengan kecepatan mendekati c akan mengalami pertambahan massa, semakin cepat benda itu bergerak maka pertambahan massanya semakin besar.

m = massa benda yang bergerak menurut pengamat diam
mo = massa benda yang sesungguhnya sebelum bergerak


- Dilatasi waktu
Benda yang bergerak dengan kecepatan mendekati c akan mengalami perubahan waktu yang lebih lambat dibanding perubahan waktu yang dialami pengamat diam.

to = waktu yang dialami oleh benda bergerak relatif terhadap pengamat diam
t = waktu yang dialami oleh pengamat diam

Contoh : Seorang astronot berusia 20 tahun pergi ke planet A dengan pesawatnya yang bergerak dengan kecepatan 0,6 c pada tahun 2050. Astronot tersebut memiliki saudara kembar yang tetap tinggal di bumi. Di bumi, 5 tahun kemudian, maka kembaran astronot itu sudah berusia 25 tahun, pada saat yang sama si astronot sampai kembali ke bumi, namun astronot tersebut masih berusia 24 tahun. Waktu yang dialami oleh astronot tersebut memang benar-benar baru 4 tahun, tapi waktu yang sudah berjalan di bumi sudah 5 tahun. Seandainya astronot membawa handphone yang memiliki kalender saat pergi ke planet A, maka ketika astronot kembali ke bumi akan terlihat bahwa kalender pada handphonenya menunjukkan saat itu tahun 2054, namun kalender yang di bumi sudah menunjukkan tahun 2055.


- Energi kinetik relativistik
Seiring dengan terjadinya dilatasi massa yaitu massa benda tersebut bertambah, tentunya energi kinetiknya juga akan bertambah. Energi kinetik yang akan digunakan dalam kasus ini bukan E=(1/2)mv² , melainkan E=mc².
Pertambahan energi kinetik benda dirumuskan seperti di bawah ini :

Catatan : Jika mau menghitung kecepatan relatif benda yang bergerak terhadap benda lain, dapat menggunakan rumus 

 Dengan va adalah kecepatan benda a. vb adalah kecepatan benda b. O adalah pengamat diam.
vab = kecepatan a relatif terhadap b
vao = kecepatan a relatif terhadap pengamat diam
vob = kecepatan o relatif terhadap b
c = kecepatan cahaya

Contoh soal :
1. Sebuah roket dengan panjang 100 m bergerak dengan kecepatan 0,6 c , berapakah panjang roket itu ketika bergerak jika dilihat oleh pengamat diam?
2. Seorang astronot bermassa 60 kg pergi ke planet B dengan kecepatan 0,8 c selama 5 tahun waktu di bumi, Berapakah massa astronot dalam perjalanannya serta waktu perjalanan yang dialami astronot sebelum sampai ke planet B?
.
.
.
.
.
Kunci Jawaban :
1. 80 m
2. 100 kg dan 3 tahun

Catatan : Hanya foton yang dapat bergerak dengan kecepatan cahaya, manusia tidak mungkin bergerak dengan kecepatan cahaya, karena jika manusia dapat melakukannya, maka waktu yang akan dialami oleh manusia tersebut = 0, atau waktu disekitarnya tidak bergerak. Maka tidak akan ada kehidupan yang dialami oleh si manusia. Sebenarnya manusia juga akan kesulitan/hampir tidak mungkin bergerak dengan kecepatan mendekati kecepatan cahaya. Karena G-force yang akan dialami oleh manusia akan sangat besar dan manusia tidak akan dapat bertahan dengan G-force yang dialaminya. Manusia di permukaan bumi biasa mengalami 1-G, dan umumnya dapat bertahan sampai dengan 5-G(misalnya naik pesawat terbang). Namun seorang pilot pesawat jet/tempur yang terlatih dapat bertahan hingga 9G sampai 10G. Namun ketika bergerak mendekati kecepatan cahaya, G-force yang akan dialami manusia >>10G , sehingga hampir tidak memungkinkan untuk manusia bergerak dengan kecepatan cahaya untuk bertahan hidup.

Sekian materinya, semoga dapat bermanfaat.

Hukum Newton

Adalah hukum dasar dalam mempelajari mekanika Newton.
Hukum Newton ada 3 yaitu Hukum I Newton, Hukum II Newton. Hukum III Newton.

Hukum I Newton
Menyatakan bahwa benda akan tetap diam atau bergerak dengan kecepatan konstan , artinya resultan gaya yang bekerja pada benda adalah 0 (ΣF=0).
Contoh :
- Sebuah kelereng yang berada di tanah dan tidak diberi gaya apapun, maka kelereng tersebut akan tetap diam dan tidak bergerak.
- Sebuah bola pejal yang bergerak dengan kecepatan konstan di lantai yang licin(tidak ada gesekan), maka bola tersebut akan terus bergerak dengan kecepatan konstan.

Hukum II Newton
Menyatakan bahwa resultan gaya yang bekerja pada benda tidak sama dengan 0 (ΣF≠0). Artinya ada gaya yang menyebabkan benda bergerak dipercepat (a bernilai positif) maupun diperlambat (a bernilai negatif). ΣF=m.a
Contoh :
- Sebuah balok bermassa 5 kg yang diam didorong dengan gaya 5 N maka balok tersebut akan bergerak dipercepat dengan percepatan 1m/s².
 ΣF=m.a
5N=5kg.a
1m/s²=a

Hukum III Newton
Menyatakan bahwa jika suatu benda memberikan sebuah gaya terhadap benda lain, maka benda lain tersebut akan memberikan gaya yang sama terhadap benda. Atau bisa dikatakan gaya aksi benda = gaya reaksi yang diterima benda. (ΣF aksi = ΣF reaksi).
Contoh :
-Balok A bermassa 1 kg bergerak dengan kecepatan konstan 5 m/s menuju ke arah balok B bermassa 2 kg yang diam. Setelah 1 detik bergerak, balok A sampai ke balok B dan menumbuk balok B dengan gaya 5 N (aksi). Pada saat yang sama balok B juga akan memberikan gaya yang sama yaitu 5N terhadap balok A (reaksi).
Catatan : Dalam mempelajari Hukum III Newton, maka harus mempelajari juga materi impuls dan momentum.
I=Δp=F.Δt
p=m.v

I=Impuls ...........(kg m/s)
p=momentum ...(kg m/s)
F=gaya .............(N)
t=waktu ............(s)
m=massa ..........(kg)
v=kecepatan .....(m/s²)

Contoh soal :
1. Benda A yang bermassa 10 kg didorong dengan gaya 20 N. Berapa percepatan yang dialami benda?
2. Sebuah bola bermassa 5 kg dijatuhkan dari ketinggian 5 m tanpa kecepatan awal. Dengan mengabaikan gesekan bola dengan udara, berapakah resultan gaya yang bekerja pada bola? (g=10m/s²)
.
.
.
.
.
Kunci jawaban :
1. 2m/s²
2. 50 N

Sekian materi hukum Newton , semoga tulisan ini dapat bermanfaat bagi pembaca sekalian.

Biologi

BIOLOGI...apa sih itu biologi?

Biologi adalah ilmu alam yang mempelajari tentang kehidupan dan organisme hidup termasuk struktur, fungsi, evolusi, pertumbuhan, dan persebarannya. Biologi menjadi dasar pokok yang harus dikuasai jika anda ingin menjadi dokter, ahli bioteknologi dan biokimia, serta beberapa profesi yang menekan pengetahuan tentang kehidupan itu sendiri.

Biologi dalam pelajaran sekolah (SD-SMP-SMA) sangat menekankan pengertian dan hafalan jenis, struktur, serta fungsi setiap jenis sel maupun organisme. Terutama dalam pelajaran SMA, hafalannya luar biasa banyak sehingga anda memerlukan trik-trik tertentu agar dapat mengingat semuanya, bisa dengan membuat analogi, lagu, dll... sesuai dengan cara belajar anda.

Untuk pembaca yang masih duduk di bangku smp dan jika ingin mengambil jurusan mipa di bangku sma, maka anda harus menguasai betul materi biologi SMP, karena jika tidak, percayalah, anda akan keteteran dalam mempelajari biologi saat berada di bangku SMA.

Biologi dalam jenjang pendidikan SMA secara garis besar mempelajari 3 materi pokok utama. Untuk kelas X akan mempelajari tentang klasifikasi, ciri-ciri, dan fungsi semua makhluk hidup selain manusia (protista,monera,fungi,plantae,animalia) dan ekosistem. Untuk kelas XI akan mempelajari tentang sel-sel dalam tubuh manusia serta cara kerjanya (sel,respirasi,koordinasi,ekskresi,sistem peredaran darah,sistem gerak,sistem imunitas,sistem saraf, dll). Sementara untuk kelas XII akan mempelajari tentang pertumbuhan&perkembangan, katabolisme&anabolisme, gen, teori evolusi, bioteknologi,dll.

Itulah sekilas tentang Biologi. Semoga dapat bermanfaat bagi pemirsa sekalian.

Fisika

Apa itu fisika? Kenapa kita harus belajar fisika?

Fisika adalah ilmu alam yang mempelajari tentang unsur-unsur dasar pembentuk alam semesta, gaya-gaya yang bekerja di dalamnya, serta akibat-akibat dari gaya-gaya tersebut. Maka dari itu, mempelajari fisika sama dengan mempelajari hal-hal yang berhubungan dengan lingkungan hidup kita, seperti cahaya, listrik, air, gas, gerak, dll. Penerapan fisika dalam kehidupan sehari-hari terutama dalam teknologi sangatlah banyak. Pada era modern saat ini, orang-orang berlomba-lomba membuat teknologi terbaru yang lebih baik, yang dapat memudahkan pekerjaan manusia sehari-hari(misalnya industri kreatif), yang semuanya itu tentunya memiliki dasar yang sama, yaitu fisika.

Fisika secara garis besar terbagi menjadi 5, yaitu : mekanika kuantum, mekanika newton, dan teori relativitas, termodinamika, dan elektromagnetik. Kalau untuk tingkat SD-SMP, biasanya siswa hanya mempelajari tentang mekanika newton, karena aplikasi mekanika newton sangat banyak ditemukan dalam kehidupan sehari-hari sehingga dapat lebih mudah dimengerti ketika dipelajari. Namun ketika masuk SMA, mekanika newton tetap akan dipelajari dan tentunya lebih dalam serta sangat dominan dalam buku fisika SMA, sementara ilmu-ilmu yang baru akan dipelajari di fisika SMA adalah mekanika kuantum, teori relativitas, termodinamika dan elektromagnetik.

- Mekanika kuantum sendiri berbicara tentang partikel-partikel yang berukuran sangat kecil seperti atom dan partikel-partikel pembentuk atom.

- Mekanika Newton mempelajari tentang dimensi, massa, gerak(posisi,kecepatan,percepatan),energi gerak, impuls, momentum, torsi, daya, usaha, dll.

- Teori relativitas (kenapa disebut teori, bukan hukum? Karena sulit dibuktikan/dilakukan percobaannya di bumi) dibagi menjadi teori relativitas umum dan teori relativitas khusus. Teori relativitas khusus mempelajari tentang benda yang bergerak mendekati kecepatan cahaya/c(300.000km/s). Sementara teori relativitas umum mempelajari tentang gaya gravitasi yang merupakan akibat dari pelengkungan ruang-waktu yang terjadi akibat adanya suatu massa. Analoginya seperti ini : Jika ada beberapa koin yang diletakkan pada suatu kain, lalu diletakkan benda bermassa besar, misal bola bowling pada kain itu, maka bola bowling itu akan menekan kain itu lebih kebawah sehingga koin-koin tersebut akan ikut jatuh ke arah pelengkungan kain yang disebabkan oleh bola bowling tersebut.

-Termodinamika sendiri mempelajari tentang panas, suhu, entropi, energi, dll.

-Elektromagnetik mempelajari tentang kelistrikan(muatan listrik, arus listrik, medan listrik,dll), dan magnetisitas(gaya magnet, medan magnet,dll) serta hubungan antara kelistrikan dan magnetisitas

Itulah sekilas tentang ilmu fisika, semoga dapat bermanfaat bagi pembaca sekalian.

Transformasi Geometri

Transformasi Geometri adalah ilmu geometri yang mempelajari tentang perpindahan suatu titik/bangun baik letaknya maupun bentuknya berdasarkan gambar/matriksnya.

Berdasarkan perpindahan letak maupun bentuknya, transformasi geometri dibagi menjadi 4 yaitu pergeseran/translasi , pencerminan/refleksi , perputaran/rotasi , perkalian/dilatasi.

1. Pergeseran/Translasi
Misalkan suatu titik P terletak pada koordinat (x,y) dan ditranslasikan terhadap titik (a,b) , maka letak hasil translasinya adalah di titik P' dengan koordinatnya (x+a , y+b).
Misalkan pula suatu fungsi y=f(x) ditranslasikan terhadap titik (a,b) , maka hasil translasinya dapat dihitung dengan rumus : (y-b)=f(x-a)

2. Pencerminan/Refleksi.
- Pencerminan titik, garis, kurva terhadap sumbu x
- Pencerminan titik, garis, kurva terhadap sumbu y
- Pencerminan titik, garis, kurva terhadap garis y=x
- Pencerminan titik, garis, kurva terhadap garis y=-x
- Pencerminan titik, garis, kurva terhadap titik (0,0)
- Pencerminan titik, garis, kurva terhadap garis y=h
- Pencerminan titik, garis, kurva terhadap garis x=h
- Pencerminan titik, garis, kurva terhadapgaris y=mx

3. Perputaran/Rotasi
Dalam transformasi geometri, jika suatu titik/bangun dirotasikan, maka arah rotasinya berlawanan dengan arah jarum jam, kecuali jika diberi keterangan pada soal bahwa rotasi searah jarum jam.
- Rotasi pada titik O (0,0)
- Rotasi pada titik Q (a,b)

4. Perkalian/Dilatasi
- Dilatasi dari titik O (0,0)
Dilatasi dari titik O (0,0) sebesar k dinotasikan [O(0,0) , k]
- Dilatasi dari Q (a,b)
Dilatasi dari titik Q (a,b) sebesar k dinotasikan [Q(a,b) , k]

Rumus-rumus pada transformasi geometri pada gambar dibawah ini :

Dengan menghafal rumus-rumus dan matriks-matriks pada transformasi geometri, maka anda dapat mengerjakan latihan soal transformasi geometri dengan lebih lancar dan semoga anda dapat menguasai materi transformasi geometri ini dengan baik.

Catatan : Jika ingin menghitung Luas bangun hasil transformasi dengan diketahui Luas bangun sebelum ditransformasi dan matriks yang akan mentransformasikannya, maka ada cara cepat yaitu :
1. Jika bangun tersebut ditransformasikan berupa translasi/refleksi/rotasi , maka luas bangun hasil transformasi=luas bangun awal(sebelum ditransformasi)
2. Jika bangun tersebut ditransformasikan berupa dilatasi sebesar k, maka luas bangun hasil transformasi=k².luas bangun awal(sebelum ditransformasi). Luasnya akan menjadi kali k² kali dari luas semula.
3. Jika bangun tersebut ditransformasikan terhadap suatu matriks acak, maka luas bangun hasil transformasi tersebut = |det matriks|.luas bangun awal(sebelum ditransformasi). Jadi luas semula dikalikan mutlak dari determinan matriks yang mentransformasikannya = luas bangun akhir.

Itulah sekilas tentang transformasi geometri. Semoga dapat bermanfaat bagi pembaca sekalian.

Bilangan

Bilangan kompleks(bilangan secara keseluruhan) secara garis besar terbagi menjadi 2 yaitu bilangan real dan bilangan imajiner. Namun dalam postingan ini, saya hanya akan membahas tentang bilangan real.

Bilangan real adalah bilangan yang dapat dinyatakan dalam bentuk desimal. Contohnya : 2 , 5,1 , 3,14 , dll. Bilangan real umumnya ditulis dalam 3 bentuk yaitu pecahan, desimal, dan persen.
Contoh bilangan dalam bentuk pecahan : 1/2 , 3/4 , 5/6, ....dst
Contoh bilangan dalam bentuk desimal : 0,5 , 0,123 , ....dst
Contoh bilangan dalam bentuk persen : 10% , 12% , 0,1% , ....dst

Bilangan real terbagi lagi menjadi 2 yaitu bilangan rasional dan bilangan irrasional.
Bilangan rasional adalah bilangan yang dapat dinyatakan dalam bentuk a/b (a dibagi b) , dengan catatan a dan b adalah bilangan bulat dan b≠0. Contohnya : 0,4 (dapat dinyatakan sebagai 2/5) , 0,123(dapat dinyatakan sebagai 123/1000). Sementara bilangan irrasional adalah bilangan yang tidak dapat dinyatakan dalam bentuk a/b (a dibagi b) , dengan catatan a dan b adalah bilangan bulat dan b≠0. Contohnya : e(bilangan natural)=2,7818... , π(pi)=3,14... , √2 , √3, dan √5.


Bilangan rasional selanjutnya dapat dibagi lagi menjadi bilangan bulat dan bilangan pecahan. Bilangan bulat contohnya : -10 , 1 , 5 , dll. Bilangan pecahan contohnya seperti 1/2 , 3/4 , 7/8 , dll.
Pada bilangan pecahan terdapat istilah pembilang dan penyebut. Pembilang adalah angka yang berada di bagian atas/angka pembagi dan penyebut adalah angka yang berada di bagian bawah/angka yang akan dibagi. Contohnya 1/2 , maka pembilangnya adalah 1 dan penyebutnya adalah 2.

Bilangan bulat selanjutnya dapat dibagi menjadi 2 yaitu bilangan negatif dan bilangan cacah. Bilangan negatif adalah bilangan bulat yang nilainya negatif seperti -1 , -2 , -100, dll.
Sementara bilangan cacah adalah bilangan bulat yang dimulai dari angka 0,1,2,3,...dst.

Bilangan cacah terbagi lagi menjadi 0 dan bilangan asli. Bilangan asli adalah bilangan yang dimulai dari angka 1,2,3,...dst.

Bilangan asli selanjutnya dapat dibagi lagi menjadi 1 , bilangan prima, dan bilangan komposit.
Bilangan prima adalah bilangan yang hanya memiliki 2 faktor yaitu 1 dan bilangan itu sendiri. Contoh bilangan prima : 2,3,5,7,11,13,17,19,...dst. Bilangan komposit adalah bilangan asli lebih besar(>) dari 1 dan bukan bilangan prima. Contoh bilangan komposit adalah 4,6,8,9,10,...dst.

Latihan soal :
1) Tuliskan bilangan 0,12 ke dalam bentuk pecahan dan persen.
2) Tuliskan bilangan 7/8 ke dalam bentuk desimal dan persen.
3) Tuliskan bilangan 25% ke dalam bentuk pecahan dan desimal.
4) Diantara bilangan dan 0,5 , √9 , dan √24 , manakah bilangan yang termasuk bilangan rasional?
5) Sebutkan bilangan prima antara 0-100. Ada berapa banyak bilangan prima diantara 0-100?

Itulah sekilas tentang bilangan. Semoga dapat bermanfaat bagi pembaca sekalian.










Kunci Jawaban :
1) 3/25 , 12%
2) 0,875 , 87,5%
3) 1/4 , 0,25
4) 0,5 dan √9 
5) 2,3,5,7,11,13,17,19,23,29,31,37,41,43,47,53,59,61,67,71,73,79,83,89,97. Ada 25 bilangan.